| Переглянути всі підручники | |||||||||||||
| << | < | 136 | 137 | 138 | 139 | 140 | 141 | 142 | 143 | 144 | 145 | > | >> |
Зведення до раціонального вигляду членів дробових ірраціональних виразів. Під час обчислення дробових ірраціональних виразів у деяких випадках доцільно звільнятись від ірраціональності (тобто від радикалів) у знаменнику або чисельнику. Це перетворення грунтується на основній властивості дробу: величина дробу не змінюється від множення його чисельника й знаменника на один й той самий вираз, який не дорівнює нулю.
Щоб піднести радикал до степеня, треба піднести до цього степеня підкореневий вираз, залишивши той самий показник радикала.
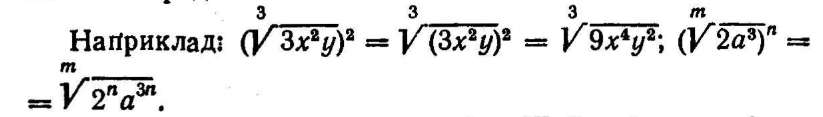
Добування кореня з радикалів. Щоб добути корінь з
кореня, достатньо з підкореневого виразу добути корінь з показником, що дорівнює добутку двох даних показників.
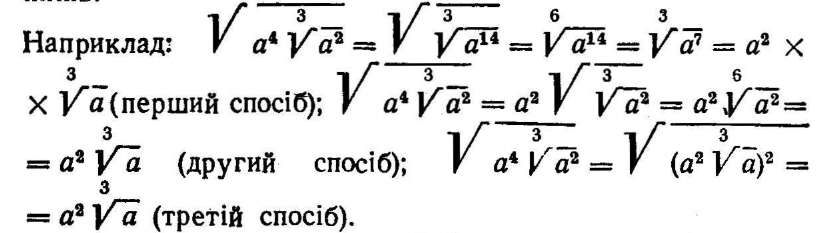
Зазначимо, що множення і ділення сум, що містять радикали, виконуються за звичайними правилами множення і ділення многочленів. При цьому щироко застосовуються формули скороченого множення і ділення. Наприклад:
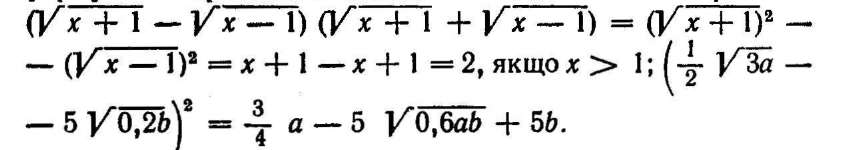
Розкладаючи на множники вирази, що містять "радикали, застосовують не тільки розкладання на множники підкореневих виразів, а й подання раціональних виразів у вигляді добутку радикалів.
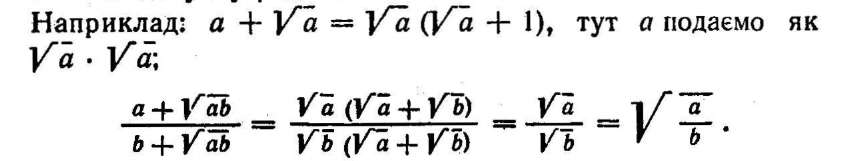
| Переглянути всі підручники | |||||||||||||
| << | < | 136 | 137 | 138 | 139 | 140 | 141 | 142 | 143 | 144 | 145 | > | >> |