| Переглянути всі підручники | |||||||||||||
| << | < | 463 | 464 | 465 | 466 | 467 | 468 | 469 | 470 | 471 | 472 | > | >> |
Підставляючи значення Р (АВ), Р (А) і Р (В) у рівність (1), дістанемо тотожність. Що і доводить справедливість теореми
Застосуємо доведену теорему до розв'язування задач.
Задача І. Завод виготовляє 95 % стандартних виробів, причому з них 86 % першого сорту. Знайти імовірність того, що виріб, виготовлений на цьому заводі, виявиться першого сорту.
Розв'язання Нехай А — подія, яка полягає в тому, що взятий виріб стандартний, В — виріб першого сорту, С — виріб, виготовлений на цьому заводі, виявився першого сорту. Тоді С = АВ.
Оскільки події А і В незалежні, то можна застосовувати теорему множення для обчислення імовірності події С.
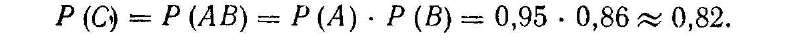
Задача 2. Імовірність отримати брак під час першої операції обробки деталі дорівнює 1 %, під час другої — 2 %, під час третьої —3 %. Знайти імовірність виготовлення небракованої деталі, якщо контроль здійснюється після трьох операцій обробки за умови незалежності виготовлення бракованої деталі під час кожної операції.
Р о з в' я з а н н я. Введемо позначення: А1 — виготовлення бракованої деталі під час 1-шої операції, A2 — виготовлення бракованої деталі під час 2-гої операції, A3 — виготовлення бракованої деталі під час 3-тьої операції, А — виготовлення небракованої деталі після трьох операцій обробки.

| Переглянути всі підручники | |||||||||||||
| << | < | 463 | 464 | 465 | 466 | 467 | 468 | 469 | 470 | 471 | 472 | > | >> |