| Переглянути всі підручники | |||||||||||||
| << | < | 458 | 459 | 460 | 461 | 462 | 463 | 464 | 465 | 466 | 467 | > | >> |
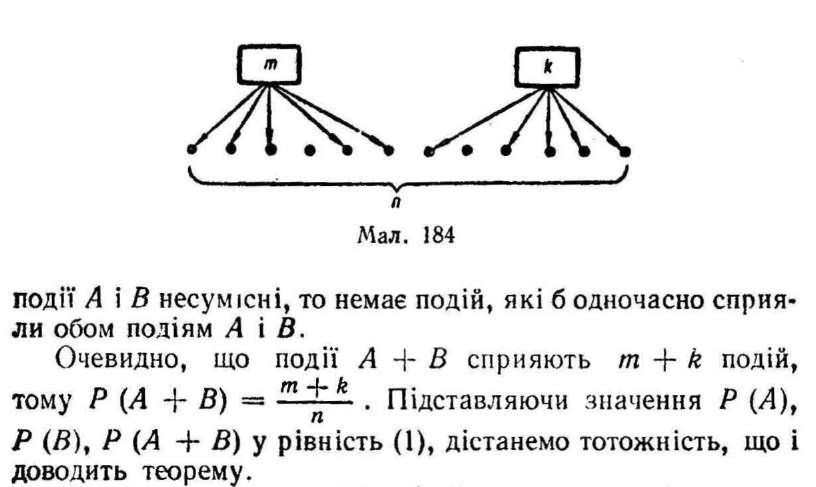
Методом математичної індукції можна довести, що теорема виконується для суми будь-якої скінченної кількості попарно несумісних подій, тобто що
Р(А1 + А2+ ... + A„) = = P (A1) +P(A2) + .... + P (A„).
Покажемо застосування теореми додавання для обчислення імовірностей складних подій.
Задача. В урні лежать 4 чорних, 7 червоних, 9 зелених і 11 синіх кульок. Звідти вийняли одну кульку. Визначити імовірність появи кольорової кульки (не чорної)
Розв'язання. Нехай подія А — поява кольорової кульки, — поява чорної, А2 — поява червоної, A3 — поява зеленої, A4 — поява синьої кульки. Тоді подію А можна виразити як суму несумісних подій А2, Aв, A4, тобто А = Аг + А3 + А,.
За теоремою додавання, дістанемо
Р(A) = Р(A2) + Р(А:3) + P[A4),
або

| Переглянути всі підручники | |||||||||||||
| << | < | 458 | 459 | 460 | 461 | 462 | 463 | 464 | 465 | 466 | 467 | > | >> |