| Переглянути всі підручники | |||||||||||||
| << | < | 457 | 458 | 459 | 460 | 461 | 462 | 463 | 464 | 465 | 466 | > | >> |
в яких складаються складені. Таке обчислення спирається на застосування теорем додавання і множення несумісних однаково можливих подій, які утворюють повну групу, тобто елементарних подій. Теореми додавання і множення доведені для елементарних подій, а для інших, які не належать до елементарних, ці теореми приймаються без доведення, тобто постулюються.
Введемо спочатку поняття про суму подій. Це поняття аналогічне поняттю суми чисел, або суми векторів, в тому розумінні, що має ті самі властивості (сполучний і переставний закони). Проте додавання подій — це не дія, а специфічна для теорії імовірностей операція, аналогічна до додавання множин.
Означення. Сумою подій А і В називається подія Є, яка полягає у здійсненні під час одиничного випробування або події А, або події В, або обох разом.
Суму двох подій позначають С — А + В, або С — A U В.
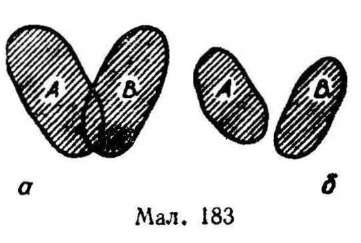
Геометрично суму подій можно зобразити так, як на малюнку 183.
Приклад. Подія А — влучення в ціль з першого пострілу, подія В — влучення з другого пострілу. Тоді С = А + В — подія, яка означає влучення в ціль взагалі (не має значення з якого — першого, другого або обох пострілів).
Суму подій А і В, як і суму множин, називають об'єднанням.
Враховуючи означення суми двох подій і поняття несумісних подій, зауважимо, що сумою С двох несумісних подій А і В є подія, яка полягає в здійсненні або події А, або події В. Одночасна поява подій А і В виключена.
Теорема. Імовірність суми двох несумісних подій дорівнює сумі імовірностей цих подій, тобто
Р (А + В) = Р (А) + Р (В). (1)

| Переглянути всі підручники | |||||||||||||
| << | < | 457 | 458 | 459 | 460 | 461 | 462 | 463 | 464 | 465 | 466 | > | >> |