| Переглянути всі підручники | |||||||||||||
| << | < | 448 | 449 | 450 | 451 | 452 | 453 | 454 | 455 | 456 | 457 | > | >> |
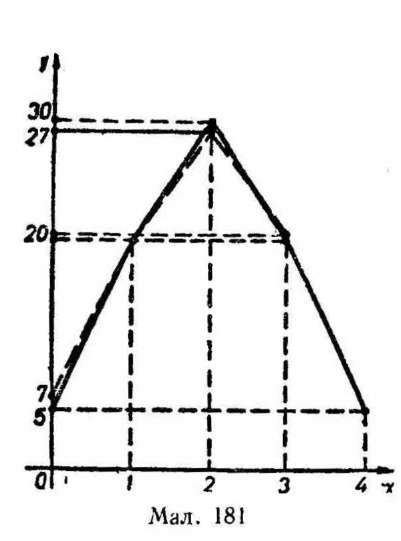
писок. Якщо в одній системі координат побудувати графік розподілу записок за результатами досліду і результатами попереднього розрахунку, то графіки мало чим відрізнятимуться один від одного (мал. 181). До того ж форма графіків нагадує розподіл шроту на дошці Гальтона.
Як бачимо, ще до проведення досліду виявилосьмож-ливим теоретичними міркуваннями передбачити його результати з невеликою похибкою. Таке передбачення е найціннішим у будь-якому науковому дослідженні і в теорії імовірностей зокрема.
Уміння передбачити хід досліду, в якому присутні елементи випадковості, дає можливість впливати на його результати. Прикладом такого передбачення може бути історія азартних ігор, які були поширені вже в XVII ст. Одна з них — гра в кості — полягала в тому, що в бокал опускали два чи три кубики, на гранях яких нанесено від однієї до шести точок. Кожний гравець по черзі викидав кості на стіл і підраховувалась сума очок,_ що. випала на верхніх гранях у кожного при певній кількості кидань. Умови виграшу були різними. Наприклад, домовл'ялись, що всю ставку отримує той, у кого загальна сума очок раніше досягне певного числа.
Для визначення шансів на виграш важливо знати, як часто випадає та чи інша кількість очок. Досвідчені гравці помітили, що при великій- кількості кидань двох костей найчастіше випадає сума очок, що дорівнює 7, а найрід-ше — 2 або 12. Враховуючи це, вони ставили такі умови гри, щоб забезпечити собі виграш, тобто впливали на хід випадкового процесу, тим самим обмежуючи вплив випадковості.
Наведені приклади показують, що в масових випадкових подіях існують закономірності.
Теорія імовірностей — математична наука, яка вивчає закономірності масових випадкових подій.
У наш час зросла роль теорії імовірностей у сучасному природознавстві. Виявляється, що відомі фізичні закони Гей-Люссака, Бойля—Маріогта, Паскаля, Авогадро та ін.
| Переглянути всі підручники | |||||||||||||
| << | < | 448 | 449 | 450 | 451 | 452 | 453 | 454 | 455 | 456 | 457 | > | >> |