| Переглянути всі підручники | |||||||||||||
| << | < | 424 | 425 | 426 | 427 | 428 | 429 | 430 | 431 | 432 | 433 | > | >> |
Перестановки. Насамперед уведемо поняття впорядкованої множини. Для цього розглянемо дві задачі.
1) 3 тридцяти учнів класу треба обрати голову і секретаря класних зборів. Скількома способами це можна зробити?
2) 3 тих же тридцяти учнів слід виділити двох для чергування в шкільній їдальні. Скількома способами це можна зробити?
Обидві задачі комбінаторні. Проте вони різні за змістом умови. У другій задачі немає значення, в якому порядку будуть названі чергові, .тоді як у першій задачгце істотно. Справді, з двох обраних учнів один може бути головою, другий — секретарем або навпаки.
Отже, під час розв'язування комбінаторних задач доводиться мати справу із скінченними множинами, для яких істотний порядок елементів. Такі множини називають впорядкованими.
Вказати порядок розташування елементів в скінченній множині з п елементів означає поставити у відповідність кожному елементу даної множини певне натуральне число від 1 до п.
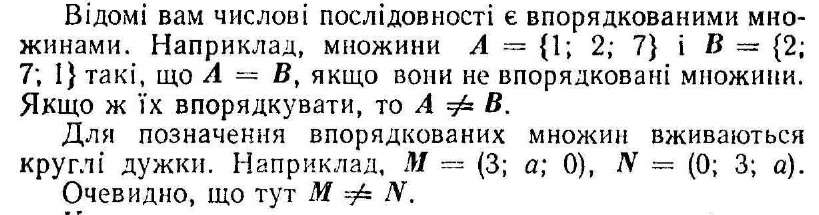
Кожну з цих двох впорядкованих множин називають перестановкоюз трьох елементів.
Означення. Будь-яка впорядкована множина, яка складається з п елементів, називається перестановкою з п елементів.
Отже, перестановки з п елементів відрізняються одна від одної лише порядком елементів.
Очевидно, що з елементів множини А = {1; 2; 7} можна утворити шість перестановок: (1; 2; 7), (1; 7; 2), (2; 1; 7), (2; 7; 1), (7; 1; 2), (7; 2; 1).
Елементи цих перестановок утворюють шість різних тризначних чисел: 127; 172; 217; 271; 712; 721.
Число перестановок з трьох елементів позначається символом Р'3, відповідно символом Рn позначається число перестановок з п елементів.
Вище ми встановили, що Р3 = 6. Виникає запитання, як знайти формулу для обчислення числа перестановок з n елементів?
| Переглянути всі підручники | |||||||||||||
| << | < | 424 | 425 | 426 | 427 | 428 | 429 | 430 | 431 | 432 | 433 | > | >> |