| Переглянути всі підручники | |||||||||||||
| << | < | 420 | 421 | 422 | 423 | 424 | 425 | 426 | 427 | 428 | 429 | > | >> |
§ 1. Поняття множини. Операції над множинами
Поняття множини належить до первісних понять математики, якому не дається означення. Множину можна уявити собі як сукупність, зібрання деяких предметів, об'єднаних задовільною характеристичною ознакою. Наприклад, множина учнів класу, множина цифр десяткової нумерації (0, 1, 2, 3, 4, 5, 6, 7, 8, 9), множина натуральних чисел, множина зернин у даному колосі, множина букв українського алфавіту, множина точок на прямій та ін.
Предмети, з яких складається множина, називаються її елементами і позначаються малими буквами латинського алфавіту. Наприклад, а = 5 — елемент множини, цифр десяткової нумерації. Для позначення множин використовують великі букви латинського алфавіту або фігурні дужки, всередині яких записуються елементи множини. При цьому порядок запису елементів не має значення. Наприклад, множину цифр десяткової нумерації можна позначити буквою М (чи будь-якою великою буквою латинського алфавіту) або записати так {1, 3, 5, 2, 4, 6, 8, 7, 9, 0}.
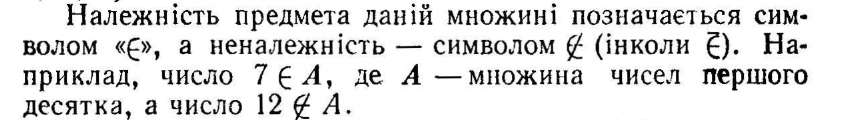
Множини бувають скінченні і нескінченні. В скінченній множині міститься певна кількість елементів, тобто кількість елементів скінченної множини виражається натуральним числом. Наприклад, множина М цифр десяткової нумерації скінченна і містить десять елементів. У нескінчен-
| Переглянути всі підручники | |||||||||||||
| << | < | 420 | 421 | 422 | 423 | 424 | 425 | 426 | 427 | 428 | 429 | > | >> |