| Переглянути всі підручники | |||||||||||||
| << | < | 504 | 505 | 506 | 507 | 508 | 509 | 510 | 511 | 512 | 513 | > | >> |
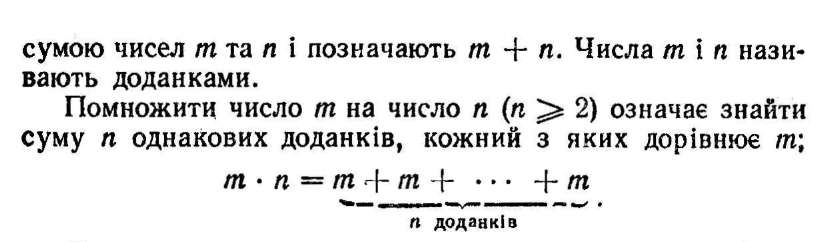
Якщо п — 1, то за означенням вважаємо, що добуток тх п дорівнює першому співмножнику т, тобтот • 1 =т.
Дії віднімання і ділення можна тлумачити як дії, обернені до додавання і множення, а саме:
1) відняти від числа т число п означає знайти таке число х, що х + п = т; число т називають зменшуваним, п — від'ємником, число х, а також вираз пі — п називають різницею;
2) розділити число т на число п означає знайти таке число х, що п • х = m; число т при цьому називають діленим, п — дільником, число х, а також вираз т : п називають часткою.
Будь-яке натуральне число можна записати у вигляді суми розрядних одиниць. Наприклад, 6 302 872 = 6 000 000 + 300 000 + 2000 + 800 + 70 + 2.
На цій властивості грунтується розрядне додавання, віднімання, множення і ділення натуральних чисел у стовпчик.
Приклади.

У множині натуральних чисел завжди можна виконувати дії додавання і множення, в результаті яких теж дістанемо натуральне число. Для цих дій виконуються переставний і сполучний закони, а також розподільний закон множення відносно додавання і віднімання: а + b= b + а, а • b — b • а, (а + b) + с = а + (b + с), (а • b) • с — а • (b • с), (а + b) • с = а • с + b • с, (а — b) • с = а • с — b • с.
| Переглянути всі підручники | |||||||||||||
| << | < | 504 | 505 | 506 | 507 | 508 | 509 | 510 | 511 | 512 | 513 | > | >> |