| Переглянути всі підручники | |||||||||||||
| << | < | 398 | 399 | 400 | 401 | 402 | 403 | 404 | 405 | 406 | 407 | > | >> |
Пропонуємо самостійно довести справедливість сполучного закону додавання для трьох комплексних чисел z1 = a + bі, z2 = с + di, z3 = l + fi.. Віднімання комплексних чисел. Віднімання комплексних чисел означають як дію, обернену до додавання, коли за даною сумою й одним з доданків знаходять другий, невідомий доданок.
Означення. Різницею двох комплексних чисел z1 = = а + bі і z2 = с + di називається таке комплексне число z3 = х + уі, яке в сумі з z2 дає z1.
Отже, z1— z2 = z3, якщо z3 + z2 = z1. Можливість дії віднімання комплексних чисел та її однозначність потребує доведення.
Доведемо, ЩО ДЛЯ будь-яких комплексних чисел z1 = = а + bі і z2 = с + di різниця z1 — z2 визначена і до того ж однозначно. Доведемо, що існує, і до того ж єдине, комплексне число z3 = x + уi, яке В сумі 3 z2 ДОрІВНЮЄ z1
За означенням дії віднімання, (с + di) + (х + уі) — = а + bі. Виконавши додавання в лівій частині рівності, дістанемо:
(с + x) + (d + у)і = а + bі. (1)
З умови рівності двох комплексних чисел маємо:
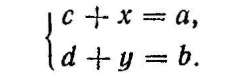
Ця система має розв'язок і до того ж єдиний: х = а — с, у — b — d. Отже, існує, і до того ж єдина, пара дійсних чисел (х, у), яка задовольняє рівняння (1), що і треба було довести. З доведеного випливає, що віднімання комплексних чисел виконують за таким правилом:
(а + bі) — (с + di) = (а — с) + (b — d) і,
тобто дійсна частина різниці двох комплексних чисел дорівнює різниці дійсних частин зменшуваного і від'ємника, а коефіцієнт при уявній частині — різниці коефіцієнтів при уявних частинах зменшуваного і від'ємника.
Приклади. Виконати віднімання комплексних чисел:
а) (3 + 4і) - (1 + 2i) = (3 — 1) + (4 — 2) i = 2 + 2i;
б) (—5 + 2i) — (2 + і) = (—5 — 2) + (2 — 1) і = = —7 + і;
в) (6 + 7i) — (6 - 5i) = (6 — 6) + (7 + 5) і == 12i,
г) (0,3 + 2,5i) — (—0,75 + 1,5i = (0,3 + 0,75) + + (2,5 - .1,5) і = 1,05 + і;
| Переглянути всі підручники | |||||||||||||
| << | < | 398 | 399 | 400 | 401 | 402 | 403 | 404 | 405 | 406 | 407 | > | >> |