| Переглянути всі підручники | |||||||||||||
| << | < | 395 | 396 | 397 | 398 | 399 | 400 | 401 | 402 | 403 | 404 | > | >> |
§ 1. Розширення МНОЖИНИ дійсних чисел. Поняття про комплексне число
У багатьох розділах математики та її застосуваннях неможливо обмежитися розглядом лише дійсних чисел Вже досить давно під час розв'язування різних задач виникла потреба добувати квадратний корінь з від'ємних чисел. Але чисел, які при піднесенні до квадрата дають від'ємні числа, тоді не знали і тому вважали, що квадратні корені 8 від'ємних чисел не існують, тобто задачі, які до них приводять, не мають розв'язків. Зокрема, так було під час розв'язування квадратних рівнянь з від'ємним дискримінантом, наприклад:
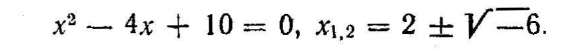
Тому природно постало питання про розширення множини дійсних чисел, приєднанням до неї нових так, щоб у розширеній множині, крім чотирьох арифметичних дій — додавання, віднімання, множення і ділення (за винятком ділення на нуль), можна було виконувати дію добування кореня Це питання було успішно розв'язане лише у XIX ст. Відповідно до прийнятих в математиці принципів розширення поняття числа при розширенні множини дійсни чисел мають задовольнятися такі вимоги:
1) означення нових чисел мусить спиратися на поняття дійсного числа, і нова множина має містити всі дійсні числа;
2) для нових чисел повинні виконуватися п'ять законів прямих арифметичних дій (пригадайте ці закони);
3) у новій числовій множині мусить мати розв'язок рівняння х2 = —1, бо в цій множині має виконуватися дія, обернена до піднесення до степеня.
Оскільки існує вимога, щоб у новій числовій множині рівняння х2 = —1 мало розв'язок, необхідно ввести деяке
| Переглянути всі підручники | |||||||||||||
| << | < | 395 | 396 | 397 | 398 | 399 | 400 | 401 | 402 | 403 | 404 | > | >> |