| Переглянути всі підручники | |||||||||||||
| << | < | 468 | 469 | 470 | 471 | 472 | 473 | 474 | 475 | 476 | 477 | > | >> |
Коли проводять серію незалежних випробувань, то практичне значення має не результат кожного окремого випробування, а загальна кількість появи серед всіх випробувань події А, яка нас цікавить. Наприклад, у серії пострілів нас цікавить не результат кожного окремого пострілу, а загальна кількість влучань.
Розв'яжемо таку задачу.
Задача 1. Виконується три незалежних постріли в мішень, імовірність влучення в яку Р « 0,8. Знайти імовірність того, що під час цих трьох пострілів буде два влучання.
Розв'язання. Нехай А — подія, яка полягає в тому, що в мішень буде два влучання і А1, Аг, А3 — влучання відповідно під час першого,, другого і третього пострілів. Подію А можна представити у вигляді суми трьох несумісних подій:
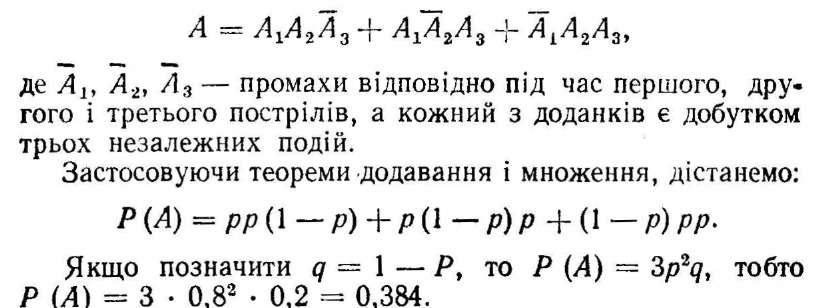
Узагальнення розв'язування задач такого виду називають схемою Бернуллі, або схемою повернутої кульки, бо будь-яку задачу, яка розв'язується за цією схемою, можна розглядати як задачу про багаторазове виймання кульки з наступним поверненням її в урну.
Задача 2. Відбувається п незалежних випробувань, у кожному з яких подія А може настати чи не настати. Імовірність здійснення події А в кожному випробуванні однакова і дорівнює р, а імовірність нездійснення події А е q = 1 — p.
Знайти імовірність Рт,п того, що подія А настане в цих п випробуваннях т разів.

| Переглянути всі підручники | |||||||||||||
| << | < | 468 | 469 | 470 | 471 | 472 | 473 | 474 | 475 | 476 | 477 | > | >> |