| Переглянути всі підручники | |||||||||||||
| << | < | 351 | 352 | 353 | 354 | 355 | 356 | 357 | 358 | 359 | 360 | > | >> |
простіших функцій, таких, як у = kx, у — хг (див. дві попередні задачі про обчислення площ). Для інших функцій, наприклад тригонометричних, обчислення границь сум ускладнюється.
Виникає запитання: чи не можна обчислювати інтеграли іншим способом? Такий спосіб був знайдений ще у XVII ст. англійським вченим Ньютоном і німецьким математиком Лейбніцем. Строге доведення формули Ньютона — Лейбніца дають у курсі математичного аналізу. Ми лише проілюструємо справедливість формули геометричними міркуваннями.
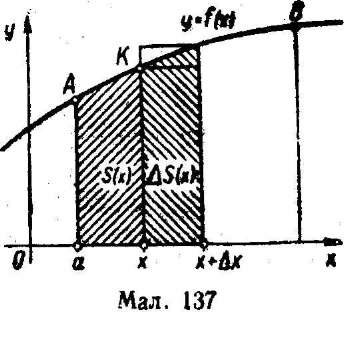
Нагадаємо задачу про площу криволінійної трапеції

| Переглянути всі підручники | |||||||||||||
| << | < | 351 | 352 | 353 | 354 | 355 | 356 | 357 | 358 | 359 | 360 | > | >> |