| Переглянути всі підручники | |||||||||||||
| << | < | 346 | 347 | 348 | 349 | 350 | 351 | 352 | 353 | 354 | 355 | > | >> |

1. Приклади задач, що приводять до поняття інтеграла. До поняття інтеграла, як і багатьох інших математичних понять, привели потреби розв'язування задач геометрії, фізики та багатьох практичних задач. Розглянемо дві такі задачі.
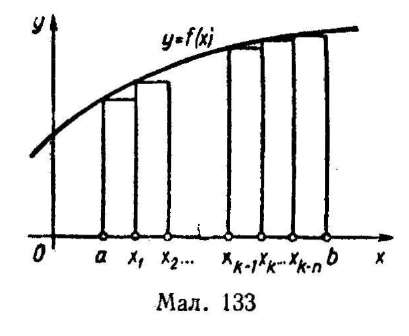
Задача 1 (про площу криволінійної трапеції"). У шкільному курсі геометрії розглядаються способи обчислення площ невеликої кількості фігур лише певного виду (многокутників, круга та його частин). Виникає запитання: як обчислити площу плоскої фігури, обмеженої будь-якою кривою? Виявляється, що розв'язування такої задачі можливе за певних умов.
Розглянемо спочатку плоску фігуру, обмежену графіком неперервної і невід'ємної на відрізку [а; b] функції у = f (х), відрізком [а; b] і прямими х = а і х = b (мал. 133). Ця фігура дістала назву криволінійної трапеції. Обчислимо ЇЇ площу.
| Переглянути всі підручники | |||||||||||||
| << | < | 346 | 347 | 348 | 349 | 350 | 351 | 352 | 353 | 354 | 355 | > | >> |