| Переглянути всі підручники | |||||||||||||
| << | < | 330 | 331 | 332 | 333 | 334 | 335 | 336 | 337 | 338 | 339 | > | >> |

Оскільки -функція Е (х) має тільки одну стаціонарну точку, а в умові задачі сказано, що існує положення лампочки, при якому освітлення в точці А найбільше,, то х е шуканою точкою.
Задача 3. Визначити розміри такого відкритого басейну з квадратним дном і об'ємом V — 32 м2, щоб на облицьовування його стін і дна було витрачено найменшу кількість матеріалу.
Роз в'якання. Позначимо довжину сторони основи через х, а висоту — через у. Тоді V (х, у) = х2у — 32.
Площа бічної поверхні басейну разом із площею дна дорівнює S = х2 + 4ху. Знайшовши з попередньої рівності у і підставивши в останню рівність його значення, дістанемо таку функцію від х:
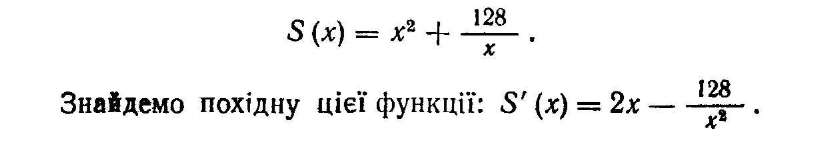
| Переглянути всі підручники | |||||||||||||
| << | < | 330 | 331 | 332 | 333 | 334 | 335 | 336 | 337 | 338 | 339 | > | >> |