| Переглянути всі підручники | |||||||||||||
| << | < | 327 | 328 | 329 | 330 | 331 | 332 | 333 | 334 | 335 | 336 | > | >> |
Зазначимо, що функція може набувати своїх найбільшого і найменшого значень як на кінцях відрізка, так і у внутрішніх його точках.
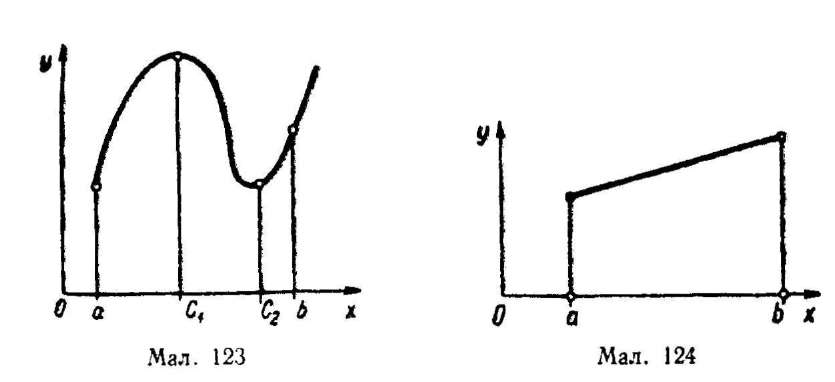
Так, на малюнку 123 зображено графік неперервної функції, яка у внутрішній точці сх відрізка [a; b] набуває найбільшого значення, а у внутрішній точці с2 — найменшого. "
На малюнку 124 зображено графік функції, яка на кінцях відрізка набуває найменшого і найбільшого значень.
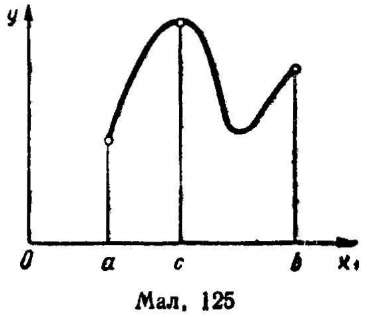
Може статися і так, що одного із значень функція набуває всередині відрізка, а другого — на одному з кінців. Так на малюнку 125 зображено графік неперервної функції, яка в лівому кінці відрізка (точці а) набуває найменшого значення, а у внутрішній точці (точці с) — найбільшого.
Якщо функція набуває найбільшого (найменшого) значення всередині відрізка, то це найбільше (найменше) значення є одночасно і локальним максимумом (мінімумом) заданої функції. Звідси випливає спосіб знаходження точок, в яких функція набуває найбільшого (найменшого) значення.
Щоб знайти найбільше (найменше) значення неперервної функції на відрізку [a; b], треба знайти всі локальні максимуми (мінімуми) і порівняти їх із значеннями функції, яких вона набуває на кінцях відрізка. Найбільше (найменше) число серед утвореної множини і буде найбільшим (найменшим) значенням функції, заданої на відрізку [а; b].
Оскільки неперервна унк-ція на відрізку [а; b] обов'язково набуває свого найбіль-
| Переглянути всі підручники | |||||||||||||
| << | < | 327 | 328 | 329 | 330 | 331 | 332 | 333 | 334 | 335 | 336 | > | >> |