| Переглянути всі підручники | |||||||||||||
| << | < | 218 | 219 | 220 | 221 | 222 | 223 | 224 | 225 | 226 | 227 | > | >> |
Взагалі те існує якогось універсального способу розв'язування логарифмічних рівнянь. Здебільшого воно зводиться до розв'язування алгебраїчних рівнянь і найпростіших логарифмічних рівнянь виду logax = b.
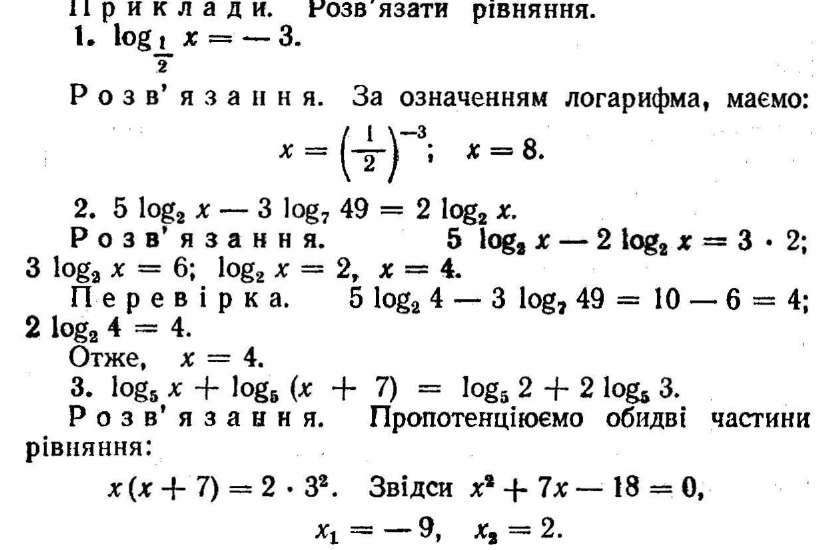
Перевірка. Підставимо в дане рівняння замість невідомого числа —9. У лівій частині дістанемо вирази log5 (—9) ' log, (—2), які не мають смислу (логарифми від'ємних чисел не існують). Отже, значення х = —9 є стороннім коренем. Тепер перевіримо, чи є коренем даного рівняння число 2. Ліва частина рівняння має вигляд:
log5 2 + log6 9 = logs 2 + log 3а = log5 2 + 2 log, 3.
Ліва частина дорівнює правій. Отже, х = 2— корінь даного рівняння.
Зауважимо, що прийом потенціювання широко застосовується під час розв'язування логарифмічних рівнянь.
4. loga (х2 + 4х + 3) = 3.
Р о з в' я з а н н я. х2 + 4х + 3 = 23, або хг + 4х — — 5 = 0. Коренями цього рівняння є: xt = —5, х2 = 1. Перевірка показує, що обидва розв'язки задовольняють дане рівняння. (Перевірку зробіть самостійно.)
5. log7 (х — 2) — log7 (х + 2) — 1 + log7 (2х — 7) = = 0.
Розв'язання. Перенесемо два останніх доданки у праву частину рівняння: log7 (х — 2) — log7 (х + 2) = = 1 — log7 (2х — 7). Беручи до уваги, що 1 = log7 7, ма-
| Переглянути всі підручники | |||||||||||||
| << | < | 218 | 219 | 220 | 221 | 222 | 223 | 224 | 225 | 226 | 227 | > | >> |