| Переглянути всі підручники | |||||||||||||
| << | < | 213 | 214 | 215 | 216 | 217 | 218 | 219 | 220 | 221 | 222 | > | >> |
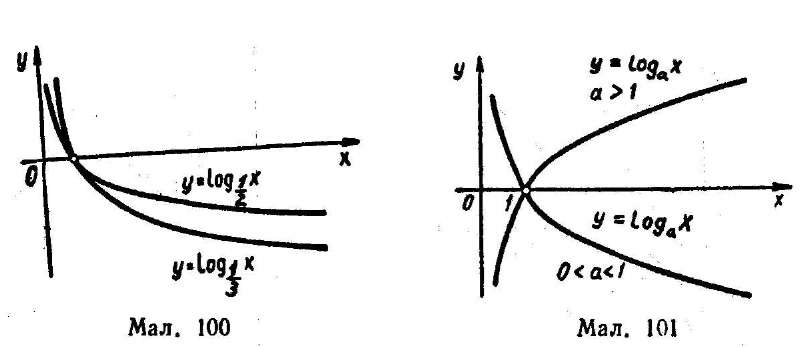
за будь-якої основи 0 < а < 1, причому крива тим щільніше прилягає до осі х, чим менше а (мал. 100).
Властивості логарифмічної функції. Знаючи властивості взаємно обернених функцій, можна легко дістати властивості логарифмічної функції з показникової. Характер графіка показникової функції за основою а залежить від того, буде а > 1 чи 0 < а < 1. Тому і характер графіка логарифмічної функції за основою а залежить від тих самих умов. Отже, для функцій у — loga х слід розрізняти 2 випадки: а > 1 і 0 < а < 1 (мал. 101). У кожному з них властивості логарифмічної функції випливають з властивостей показникової, якщо врахувати ще зв'язок між графіками показникової й логарифмічної функцій. Отже, маємо такі властивості логарифмічної функції.
1) Область визначення логарифмічної функції — множина всіх додатних чисел.
2) Область значень логарифмічної функції — множина всіх дійсних чисел.
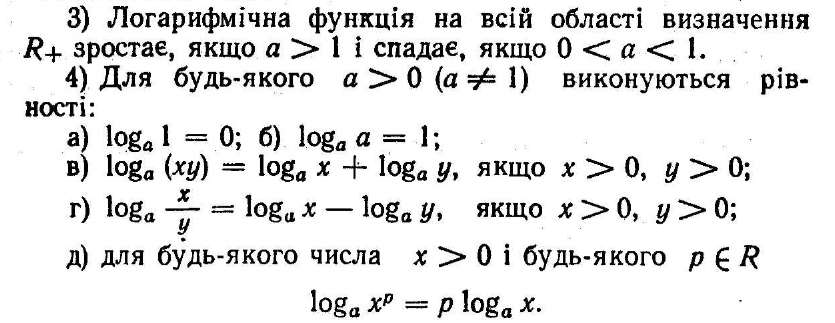
Для порівняння наведемо властивості показникової І логарифмічної функцій у вигляді таблиці (див. с. 219).
Систематизуємо властивості логарифмів, які слід запам'ятати, щоб впевнено використовувати їх під час
| Переглянути всі підручники | |||||||||||||
| << | < | 213 | 214 | 215 | 216 | 217 | 218 | 219 | 220 | 221 | 222 | > | >> |