| Переглянути всі підручники | |||||||||||||
| << | < | 538 | 539 | 540 | 541 | 542 | 543 | 544 | 545 | 546 | 547 | > | >> |
знаменник і перший результат записати як чисельник, а другий — як знаменник.
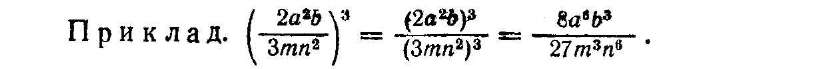
Щоб розділити один алгебраїчний дріб на другий, треба перший дріб помножити на дріб, обернений до другого:
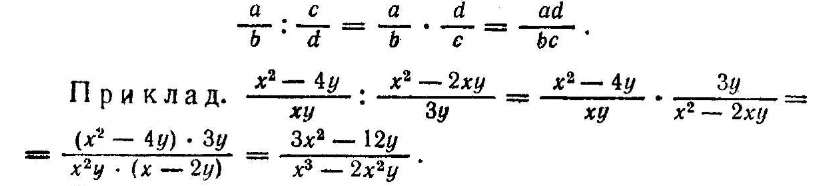
. Основна задача тотожних перетворень раціональних виразів загального виду, що містять цілі і дробові вирази, полягає в зведенні виразу до дробу, у якого чисельник і знаменник — многочлени стандартного вигляду. При цьому порядок виконання перетворень такий самий, як і порядок виконання дій у числових виразах.

4. Ірраціональні вирази. Квадратний корінь і його властивості. Квадратним коренем з числa a називаються числа, квадрати яких дорівнюють a. Наприклад, числа 4 і —4 — квадратні корені з числа 16, оскільки 42 = 16 і (—4)2 = 16. Квадратний корінь з числа 0 дорівнює 0. Корінь з числа 0 є єдиним, оскільки у множині дійсних чисел тільки 02 = 0.
Квадратного кореня з від'ємного числа не існує, оскільки у множині дійсних чисел не існує числа, квадрат якого дорівнював би від'ємному числу. Наприклад, не існує квадратного кореня з числа —25, оскільки при множенні дійсних чисел не існує числа, квадрат якого дорівнював би —25.
| Переглянути всі підручники | |||||||||||||
| << | < | 538 | 539 | 540 | 541 | 542 | 543 | 544 | 545 | 546 | 547 | > | >> |