| Переглянути всі підручники | |||||||||||||
| << | < | 536 | 537 | 538 | 539 | 540 | 541 | 542 | 543 | 544 | 545 | > | >> |
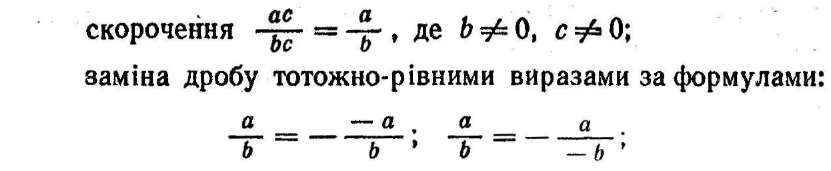
зведення їх до спільного знаменника;
перетворення суми і різниці, добутку, частки, степеня дробів у дріб, чисельник і знаменник якого — многочлени стандартного вигляду.
Як правило, алгебраїчні дроби намагаються звести до простішого спільного знаменника. Щоб знайти простіший спільний знаменник двох або кількох дробів треба:
1) скласти добуток найменшого спільного кратного коефіцієнтів знаменників даних дробів і степенів кожної змінної (букви) з найбільшим показником, який має змінна у знаменниках даних дробів;
2) знайти додатковий множник кожного з даних дробів; для цього слід представити спільний знаменник у вигляді добутку двох одночленів, з яких один — знаменник даного дробу, тоді другий буде її додатковим множником;
3) знайти добуток чисельника кожного дробу на додатковий множник і записати спільний знаменник.

Додавання і віднімання алгебраїчних дробів з однаковими знаменниками здійснюють аналогічно до виконання цих дій для звичайних дробів.
Щоб додати (відняти) алгебраїчні дроби з однаковими знаменниками, треба записати у чисельнику суму (різницю)
| Переглянути всі підручники | |||||||||||||
| << | < | 536 | 537 | 538 | 539 | 540 | 541 | 542 | 543 | 544 | 545 | > | >> |