| Переглянути всі підручники | |||||||||||||
| << | < | 493 | 494 | 495 | 496 | 497 | 498 | 499 | 500 | 501 | 502 | > | >> |
впіл, так що одна половина значень більша від медіани, а друга — менша.
Якщо дані містять непарне число різних значень, наприклад 9, 11, 15, 18, 20, то медіана є середнім значенням для випадку, коли вони впорядковані, тобто медіана дорівнює 15. Якщо дані містять парне число різних випадків, наприклад 7, 11, 13, 15, то медіана дорівнює середньому між двома центральними значеннями, якщо вони впорядковані, тобто (11 + 13) : 2 = 12.
1. Знайти медіану сукупності даних;
а) 12, 2, 9, 11, 15, 24, 10;
б) 18, 43, 24, 17, 21, 26.
Р о з в* я з а н н я. а) Розмістимо дані сукупності в порядку зростання: 2, 9, 10, 11, 12, 15, 24; /1 = 7 — непарне число. Me = 11.
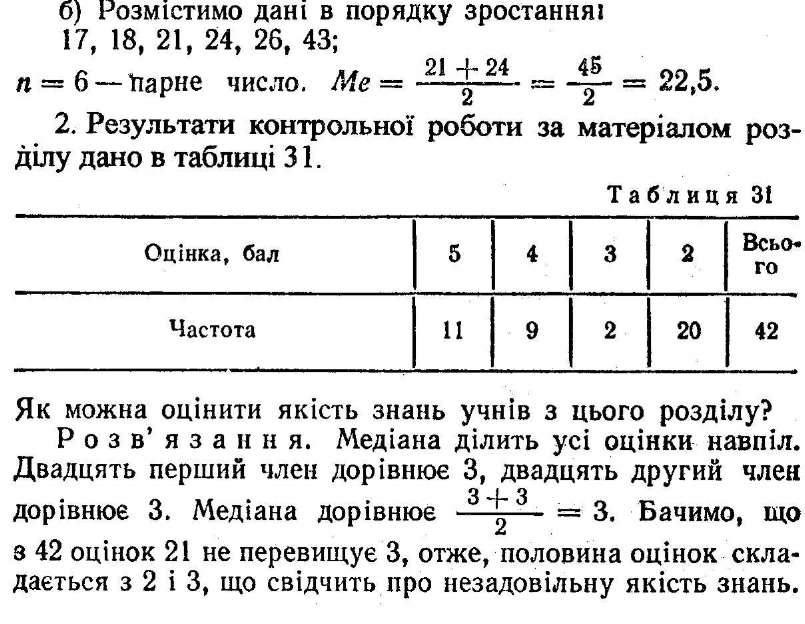
Статистика оперує такими середніми значеннями; середнє арифметичне, середнє квадратичне, середнє геометричне.
Середне арифметичне. Нехай ми маємо п об'єктів, у яких виміряно деяку характеристику, що має значення x1, x2,.., хn.
| Переглянути всі підручники | |||||||||||||
| << | < | 493 | 494 | 495 | 496 | 497 | 498 | 499 | 500 | 501 | 502 | > | >> |