| Переглянути всі підручники | |||||||||||||
| << | < | 360 | 361 | 362 | 363 | 364 | 365 | 366 | 367 | 368 | 369 | > | >> |

Приклад 9. Знайти формулу об'єму кругового циліндра з площею основи S і висотою Н.
Розв'язання. У кругового циліндра (похилого чи прямого) (мал. 150, а, б) будь-яка площа паралельних перерізів стала і дорівнює S. Тому координатну пряму Ох проведемо перпендикулярно до площини основи, а точку відліку виберемо в точці її перетину з площиною основи. В сь Ох перетне площину другої основи в точці Н, де H — висота циліндра. Тоді
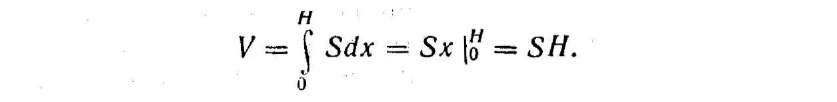
Формула V — SH виявилась однаковою і для похилого, і для прямого кругового циліндра.
Приклад 10. Знайти формулу об'єму піраміди з площею основи S і висотою Н.
Розв' язання. Нехай координатна пряма Ох проходить через вершину піраміди перпендикулярно до площини її основи (мал. 151). Виберемо за точку відліку вершину піраміди.
Перетнемо піраміду площиною, паралельною площині основи на відстані х від вершини. Площа перерізу є функ-
| Переглянути всі підручники | |||||||||||||
| << | < | 360 | 361 | 362 | 363 | 364 | 365 | 366 | 367 | 368 | 369 | > | >> |