| Переглянути всі підручники | |||||||||||||
| << | < | 288 | 289 | 290 | 291 | 292 | 293 | 294 | 295 | 296 | 297 | > | >> |
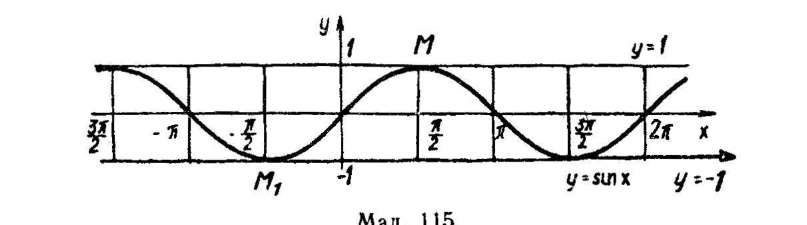
Розглянемо ще один лриклад. Нехай роглядувана крива є синусоїдою у — — sin х (мал. 115). Тоді пряма у= 1 має з даною кривою безліч спільних точок (а не одну!), і вона є дотичною до даної кривої, наприклад, у точці М. Це саме стосується і прямої у = —1, яка є дотичною до кривої, наприклад, у точці М1 і має безліч спільних точок з кривою.
Тому, як випливає із наведених прикладів, слід дати загальне означення дотичної, яке б охоплювало як замкнені, так і незамкнені криві.
Отже, нехай маємо деяку довільну криву L (мал. 116). Візьмемо на ній дві точки М0 і Мх і через них проведемо пряму М0М1, яку називатимемо січною. Якщо тепер точка Af, рухатиметься уздовж кривої, то січна M0M1 повертатиметься навколо точки М0. Нехай точка М1 рухаючись вздовж кривої, наближається до точки М0. Тоді довжина хорди М0М1 прямує до нуля. Якщо при цьому й величина кута МХМ0Т прямує до нуля, то пряма М0Т називається граничним положенням січної М0М1.
Отже, маємо таке означення.
Дотичною до кривої L у точці М0 називається граничне положення М0Т січної M0M,, якщо точка Мг прямує вздовж кривої до злиття з точкою М0.
Зазначимо, що з якого б боку точка М1 не наближалася по кривій до точки М0, січна М0М1 при цьому має наближатися до того самого її граничного положення (до тієї самої прямої). Тільки у цьому разі кажуть, що у точці MQ крива має дотичну. Не кожна крива у розглядуваній точці має дотичну. Граничного положення січної може і не існувати.
Із малюнка видно, що з якого боку точка М1 по кривій не рухалась би до точки М0, січна М0М1, обертаючись на-
| Переглянути всі підручники | |||||||||||||
| << | < | 288 | 289 | 290 | 291 | 292 | 293 | 294 | 295 | 296 | 297 | > | >> |