| Переглянути всі підручники | |||||||||||||
| << | < | 375 | 376 | 377 | 378 | 379 | 380 | 381 | 382 | 383 | 384 | > | >> |
ПОХІДНА І ПЕРВІСНА ПОКАЗНИКОВОЇ, ЛОГАРИФМІЧНОЇ ТА СТЕПЕНЕВОЇ ФУНКЦІЙ
§ 1. Похідна показникової функції
Вивчаючи показникову функцію, ми переконалися в тому, що графіки показникових функцій зображувалися у вигляді гладких кривих (без зламів), до яких у кожній точці можна провести дотичну. Відомо також, що існування дотичної до графіка функції в точці рівносильне її диферен-ційовності у цій точці. У вищій математиці доведено,, що показникова функція диференційовна у кожній її точці, і похідну показникової функції за основою е обчислюють дуже просто, а саме:
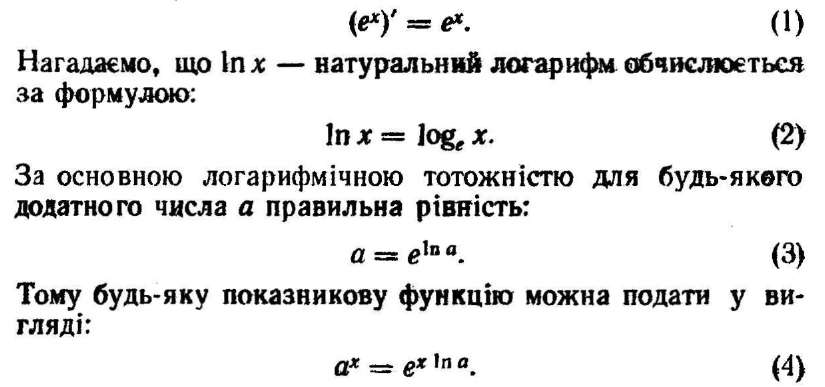
Для цього слід піднести до степеня х обидві частини рівності (3). За допомогою формули (4), застосовуючи правило обчислення похідної складеної функції, дістанемо формулу для похідної будь-якої показникової функції для будь-якого показника х:
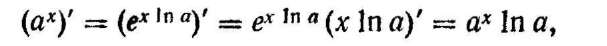
| Переглянути всі підручники | |||||||||||||
| << | < | 375 | 376 | 377 | 378 | 379 | 380 | 381 | 382 | 383 | 384 | > | >> |