| Переглянути всі підручники | |||||||||||||
| << | < | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | > | >> |
Якщо а збільшується від я д 2л (III і IV чверті), абсциса збіль-шується від —1 до 1, тобто пр зростанні аргументу від я до 2; функція косинус зростає від — до 1.
Аналогічно досліджують змін функції, синус.
Характер зміни тангенса і ко-тангенса легко дослідити, користу-ючись лініями тангенса і котан-генса.
Приклад 4. Дослідити знаки синуса і котангенса у кожній з чотирьох координатних чвертей.
Розв' язання. Можна скористатися одиничним колом і означенням синуса числа. Відомо, що ординати точок у І і II чвертях додатні, тому синус чисел а, для яких відповідна точка Ра належить І і II чвертям, додатний.
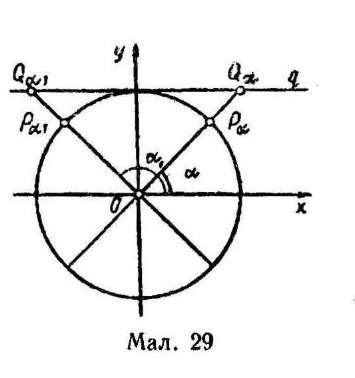
Досліджуючи знак котангенса, можна скористатися лінією котангенса (мал. 29). Якщо врахувати, що значення котангенса додатні на промені, який розміщено справа від осі Оу, і від'ємні на промені, який розміщено зліва від осі Оу, то для чисел а, відповідна точка яких Ра належить І і III чвертям, котангенс додатний, а для тих, що Ра належить II і IV чвертям,— від'ємний.
Можна дослідити знак котангенса інакше: попередньо дослідити знаки синуса і косинуса. Тоді за означенням неважко встановити знаки котангенса.
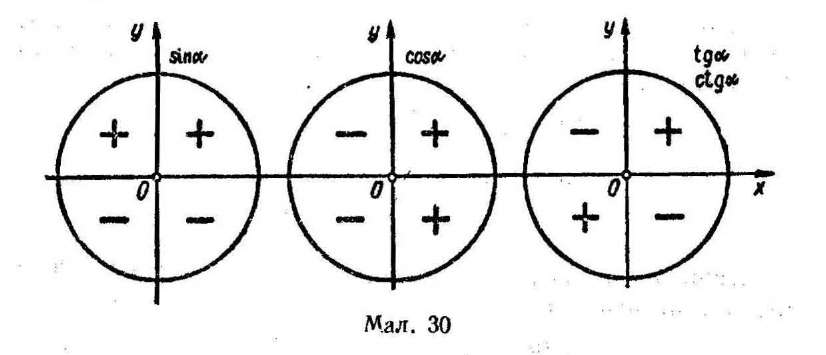
Знаки тригонометричних функцій у координатних чвертях схематично показано на малюнку 30.
Приклад 5. На одиничному колі побудувати такі кути а, що: а) sin a = —1; б) cos a = 0,5; в) tg a = 1,5; г) ctg a = —2.
| Переглянути всі підручники | |||||||||||||
| << | < | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | > | >> |