| Переглянути всі підручники | |||||||||||||
| << | < | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | > | >> |
§ 8. Співвідношення між тригонометричними функціями одного й того самого аргументу
Під час вивчення тригонометричних функцій гострого кута у 8-му класі за теоремою Піфагора було доведено основну тригонометричну тотожність
sin2 a -f cos2 а = 1. (1)
Вона виконується для тригонометричних функцій будь-якого кута і тригонометричних функцій довільного числового аргументу. Доведемо це. Якщо косинус числа а — це абсциса точки Ра одиничного кола, а синус числа а — ордината цієї точки, тобто х = cos а, у — sin а, то точка Ра (х; у) віддалена від центра кола на відстань, що дорівнює 1. Відомо, що відстань точки від початку координат визначається за формулою х2 + У2 = r2. Оскільки r = 1, то х2 + у2 = 1, тобто sin2 а + cos2 а = 1.
Означивши тангенс і котангенс через синус і косинус, ми ввели ще два незалежних співвідношення:
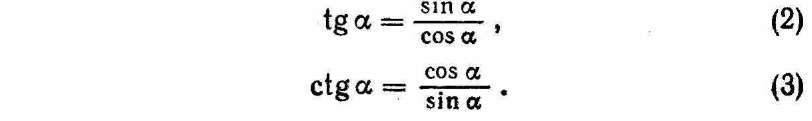
З тотожностей (1) — (3) як наслідок випливають ще кілька співвідношень, які часто використовують при обчисленні значень тригонометричних функцій через дане значення однієї з них та в інших задачах.
Перемноживши почленно рівності (2) і (3), дістанемо tg а • ctg а — 1, звідки

| Переглянути всі підручники | |||||||||||||
| << | < | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | > | >> |