| Переглянути всі підручники | |||||||||||||
| << | < | 302 | 303 | 304 | 305 | 306 | 307 | 308 | 309 | 310 | 311 | > | >> |
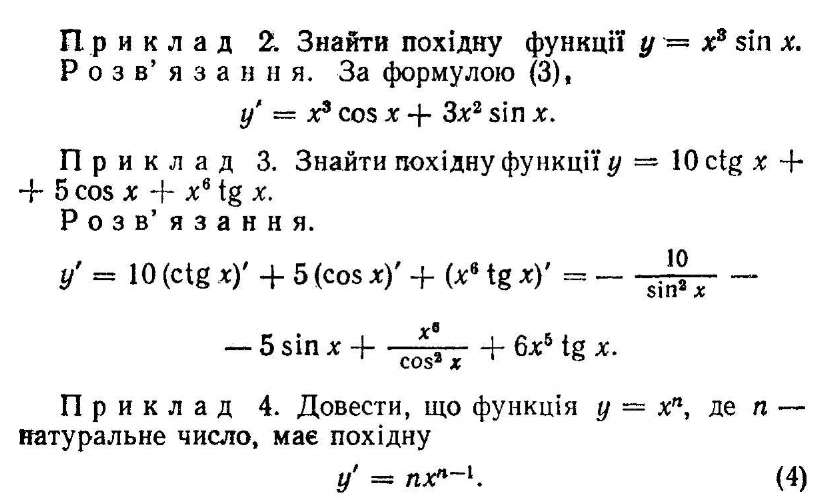
Розв'язання. Скористаємося методом математичної індукції. Цей метод грунтується на такому принципі: якщо деяке твердження А (n) відносно натурального числа п правильне для я = 1 і з припущення, що воно правильне для п = k, випливає, що воно правильне для наступного числа п = k + 1, то це твердження правильне для будь-якого натурального числа п.
Щоб довести твердження методом математичної індукції, треба:
1) перевірити правильність твердження для n = 1;
2) припустити, що воно правильне для k, і на підставі цього припущення і вже відомих тверджень довести, що твердження правильне для п — k + 1;
3) зробити висновок, що згідно з принципом математичної індукції доводжуване твердження правильне для будь-якого натурального числа п.
Доводжувана формулі у' = (хп)' — пхп–1 є твердженням відносно натурального числа п. Виконаємо три кроки:
1) переконаємося, що формула правильна для n = 1. У § 3 було доведено, що у' — (x)' = 1. Отже (х1)' = 1 X X х]–1 — х° = 1, тобто для n = 1 формула (4) правильна;
2) припустимо, що формула (4) правильна для n = k, тобто у' = (xk)' — kxk–1 і доведемо, що формула (4) правильна для п = k + 1.
Справді, використовуючи теорему про похідну добутку двох функцій і припущення, дістанемо,
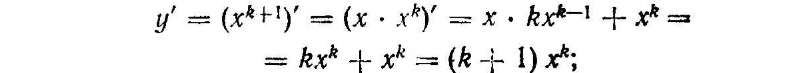
| Переглянути всі підручники | |||||||||||||
| << | < | 302 | 303 | 304 | 305 | 306 | 307 | 308 | 309 | 310 | 311 | > | >> |