| Переглянути всі підручники | |||||||||||||
| << | < | 269 | 270 | 271 | 272 | 273 | 274 | 275 | 276 | 277 | 278 | > | >> |
Оскільки число є може бути як завгодно малим, то з попередньої нерівності випливає, що значення нескінченно малої функції поблизу даної точки х0 за модулем як завгодно малі. Але не слід плутати нескінченно малу функцію в точці з досить малим числом. Значення нескінченно малої функції можуть бути за певних значень як завгодно великими числами. Наприклад, функція у = х в точці х = 0 є нескінченно малою, але її значення при досить великих за модулем значеннях х є теж як завгодно великі.
Нескінченно малі функції, аналогічно до нескінченно малих числових послідовностей, мають властивості, які ми сформулюємо у вигляді теорем.
Теорема 1. Сума (різниця) двох нескінченно малих функцій у даній точці є нескінченно малою функцією.
Цю теорему пропонуємо довести самостійно.
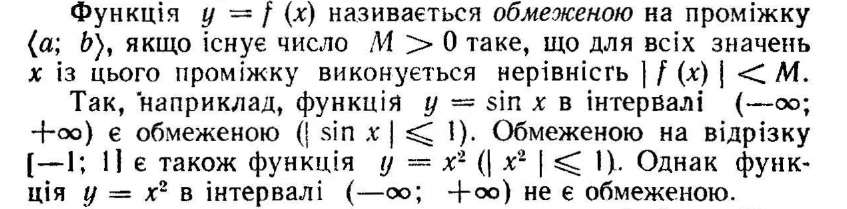
Теорема 2. Добуток нескінченно малої функції на обмежену функцію є функцією нескінченно малою у даній точці.

| Переглянути всі підручники | |||||||||||||
| << | < | 269 | 270 | 271 | 272 | 273 | 274 | 275 | 276 | 277 | 278 | > | >> |