| Переглянути всі підручники | |||||||||||||
| << | < | 228 | 229 | 230 | 231 | 232 | 233 | 234 | 235 | 236 | 237 | > | >> |
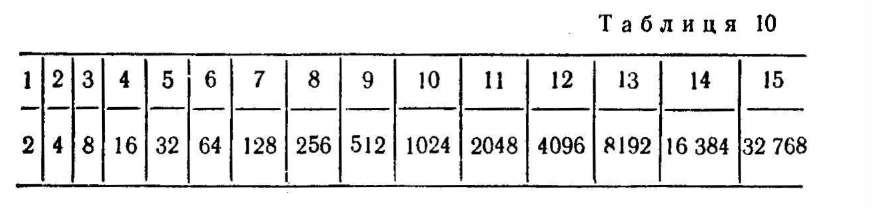
У верхньому рядку маємо арифметичну прогресію з різницею, що дорівнює 1, а в нижньому рядку — відповідно геометричну прогресію із знаменником 2. Зіставивши числа у відповідних колонках, помічаємо, що в першому рядку ми маємо логарифми чисел другого рядка за основою 2. Так, наприклад, log2 512= 9 (бо 29 512), log2 8192 = ІЗ (бо 213 = 8192) і т. д.
Користуючись даними таблиці і теоремою про те, що логарифм добутку дорівнює сумі логарифмів співмножників, можна значно спростити знаходження добутків чисел, записаних у нижньому рядку таблиці.
Нехай треба, наприклад, помножити 64 на 512. Знайдемо логарифм цього добутку за основою 2. Маємо log2 (64 • 512) = log2 64 + + log2 512. За таблицею знаходимо Iog2 64 = 6, log2 512 = 9. Отже, log2 (64 • 512) = 6 + 9 = 15. Але числу 15 з першого рядка відповідає число 32 768 з другого рядка. Отже, 64 • 512 = 32 768.
Застосовуючи теорему про логарифм частки (дробу) можна скористатися таблицею і під час ділення чисел.
Наприклад, треба поділити 8192 на 128. Знайдемо логарифм цієї частки за основою 2. Маємо:
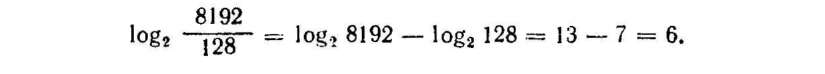
Але числу 6 з першого рядка в другому рядку відповідає число 64. Отже: 8192 : 128 = 64.
Можна скористатися таблицею і для піднесення чисел до степеня. Наприклад, обчислимо 45. Маємо log2 45 = 5 log2 4=5-2= 10. Числу 10 з першого рядка таблиці відповідає число 1024 з другого рядка. Отже, 45 = 1024.
Як бачимо, дії другого ступеня (множення, ділення) звелися до дій першого ступеня (додавання, віднімання) над відповідними логарифмами. При цьому довелося виконувати дії із значно меншими числами.
Для практичного здійснення ідеї Штіфеля треба було скласти геометричну прогресію, яка б зростала дуже повільно, бо лише при цьо-
і арифметичної прогресій. Ця ідея бере свій початок у працях А р х і -мела (бд. 287—212 до н. е.).
Розглянемо цю ідею на такому прикладі. Складемо таблицю.
| Переглянути всі підручники | |||||||||||||
| << | < | 228 | 229 | 230 | 231 | 232 | 233 | 234 | 235 | 236 | 237 | > | >> |